————— 第二天 —————



算法题目:
给定一个正整数,实现一个方法来求出离该整数最近的大于自身的“换位数”。
什么是换位数呢?就是把一个整数各个数位的数字进行全排列,从而得到新的整数。例如53241和23541。
小灰也不知道这种经过换位的整数应该如何称呼,所以姑且称其为“换位数”。
题目要求写一个方法来寻找最近的且大于自身的换位数。比如下面这样:
输入12345,返回12354
输入12354,返回12435
输入12435,返回12453


小灰发现的“规律”:
输入12345,返回12354
12354 – 12345 = 9
刚好相差9的一次方
输入12354,返回12435
12435 – 12354 = 81
刚好相差9的二次方
所以,每次计算最近的换位数,只需要加上9的N次方即可?




————————————





举一个栗子:
给定1,2,3,4,5这几个数字。
最大的组合:54321
最小的组合:12345

比如给定整数12354,如何找到离它最近且大于它的换位数呢?
为了和原数接近,我们需要尽量保持高位不变,低位在最小的范围内变换顺序。
那么,究竟需要变换多少位呢?这取决于当前整数的逆序区域。

如果所示,12354的逆序区域是最后两位,仅看这两位已经是当前的最大组合。若想最接近原数,又比原数更大,必须从倒数第3位开始改变。
怎样改变呢?12345的倒数第3位是3,我们需要从后面的逆序区域中寻找到刚刚大于3的数字,和3的位置进行互换:
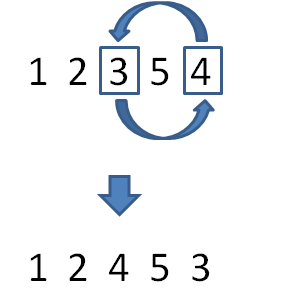
互换后的临时结果是12453,倒数第3位已经确定,这时候最后两位仍然是逆序状态。我们需要把最后两位转变回顺序,以此保证在倒数第3位数值为4的情况下,后两位尽可能小:
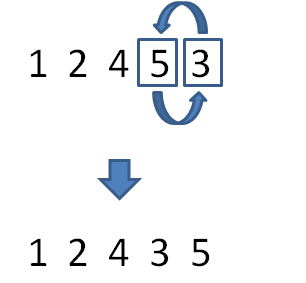
这样一来,我们就得到了想要的结果12435。


获得最近换位数的三个步骤:
1.从后向前查看逆序区域,找到逆序区域的前一位,也就是数字置换的边界
2.把逆序区域的前一位和逆序区域中刚刚大于它的数字交换位置
3.把原来的逆序区域转为顺序

- //主流程,返回最近一个大于自身的相同数字组成的整数。
- public static int[] findNearestNumber(int[] numbers){
- //拷贝入参,避免直接修改入参
- int[] numbersCopy = Arrays.copyOf(numbers, numbers.length);
- //1.从后向前查看逆序区域,找到逆序区域的前一位,也就是数字置换的边界
- int index = findTransferPoint(numbersCopy);
- //如果数字置换边界是0,说明整个数组已经逆序,无法得到更大的相同数字组成的整数,返回自身
- if(index == 0){
- return null;
- }
- //2.把逆序区域的前一位和逆序区域中刚刚大于它的数字交换位置
- exchangeHead(numbersCopy, index);
- //3.把原来的逆序区域转为顺序
- reverse(numbersCopy, index);
- return numbersCopy;
- }
- private static int findTransferPoint(int[] numbers){
- for(int i=numbers.length-1; i>0; i–){
- if(numbers[i] > numbers[i-1]){
- return i;
- }
- }
- return 0;
- }
- private static int[] exchangeHead(int[] numbers, int index){
- int head = numbers[index-1];
- for(int i=numbers.length-1; i>0; i–){
- if(head < numbers[i]){
- numbers[index-1] = numbers[i];
- numbers[i] = head;
- break;
- }
- }
- return numbers;
- }
- private static int[] reverse(int[] num, int index){
- for(int i=index,j=num.length-1; i<j; i++,j–){
- int temp = num[i];
- num[i] = num[j];
- num[j] = temp;
- }
- return num;
- }
- public static void main(String[] args) {
- int[] numbers = {1,2,3,4,5};
- for(int i=0; i<10;i++){
- numbers = findNearestNumber(numbers);
- outputNumbers(numbers);
- }
- }
- //输出数组
- private static void outputNumbers(int[] numbers){
- for(int i : numbers){
- System.out.print(i);
- }
- System.out.println();
- }
这种解法拥有一个高大上的名字:字典序算法。